Jarvis March Visualization
Brief description of the Algorithm
Jarvis march is a simple algorithm to find the convex hull of a set of points by iteratively
finding the least counter clockwise point from a given origin at every step, much like wrapping
a gift around a box, with the points of the convex hull marking its corners, where the next
corner to be wrapped becomes the next origin. We keep wrapping around the points until we return
to the initial origin.
Step-by-step Visualization
Step 1:

In the first step of the Jarvis March algorithm, we declare an arbitrary point that is outside the set S. We call this point O_init and in our implementation we have declared this random point as a point that is one unit away in x,y coordinates of the point in S with with minimum x and y coordinate.
Step 2:
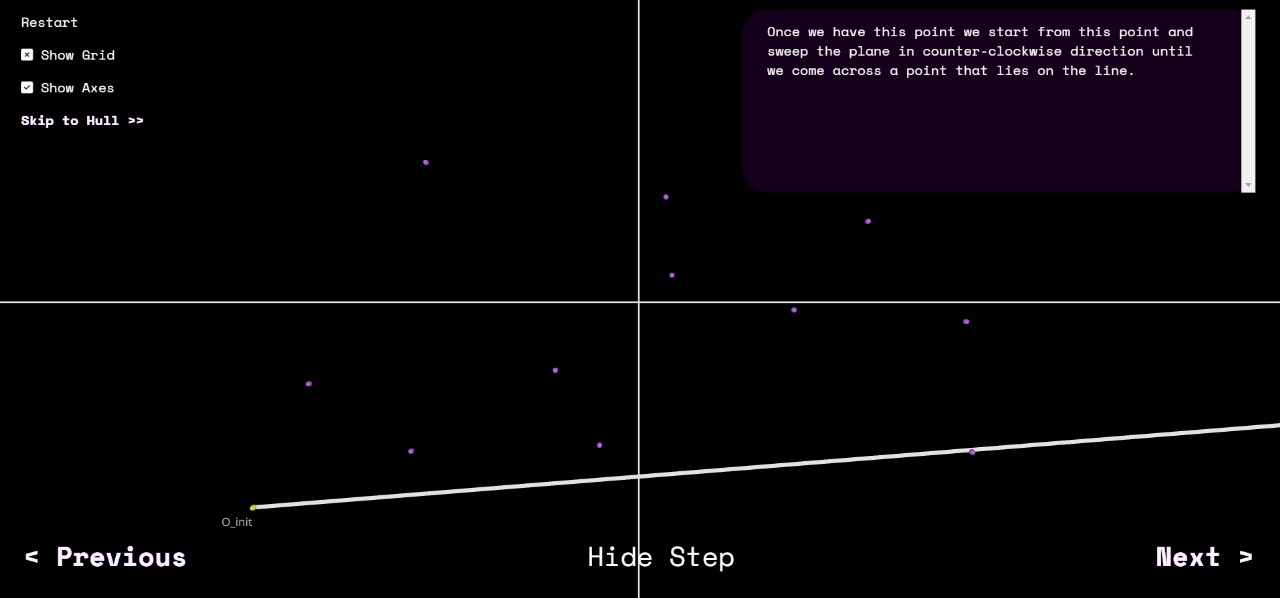
Once we have this point, we start from this point and sweep the point radially in counter-clockwise direction until we come across a point that lies on the radius. In case there is more than one point on the line, take the one closest to the current origin.
Step 3:

Once we find this point, we set this point as our origin and sweep the plane again in the same counter-clockwise direction to look for the next point that lies on the line as it keeps rotating. An important thing to remember is that, when multiple points are lying on the line, we chose the point closest to the current origin.
Step 4:
We repeat this entire process until we return back to the first origin we discovered.

Step 5:

We repeat this entire process until we return back to the first origin we discovered.
Step 6:
This is the Convex Hull of the given points using the Jarvis March algorithm.
