Analysis of Jarvis March and Kirkpatrick-Seidel
This is a side-by-side comparison of 2 Convex Hull algorithms: Jarvis March and Kirkpatrick-Seidel algorithm.
Jarvis March, also called Gift-wrapping algorithm was published in 1973. It is a simple solution
to the convex hull problem. It aims to iteratively find the least clockwise point from a given origin,
sweeping radially in anti-clockwise direction until you find the new origin, thereby covering the Convex
Hull points in order. It is analogous to how the edges of a box get covered one by one when a box is gift wrapped.
Kirkpatrick-Seidel is a slightly more efficient way of approaching the Convex Hull problem, particularly
in dealing with situations with collinear points. It is a Divide and Conquer approach that proceeds as follows:
The set of points is divided into two sets by a median line. We then find all the edges of the convex-hull that
intersect the median line, and discard points that cannot be a part of the convex-hull, with atleast a quarter
of the total points being discarded in a single iteration. Finally, we recursively call the algorithm on the
reduced search space.
To perform the analysis, first we consider 5 sets of points and run both the Convex Hull algorithms on each set and
compare the runtime of the 2 algorithms. We will also analyze the asymptotic time complexity of the algorithms.
RESULTS
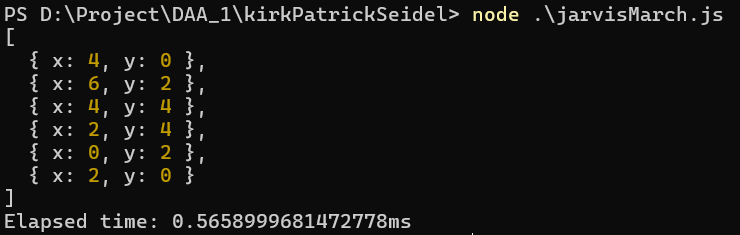
Input Points:
{ x: 0, y: 2 }, { x: 4, y: 4 }, { x: 4, y: 0 }, { x: 6, y: 2 }, { x: 2, y: 4 }, { x: 2, y: 0 }

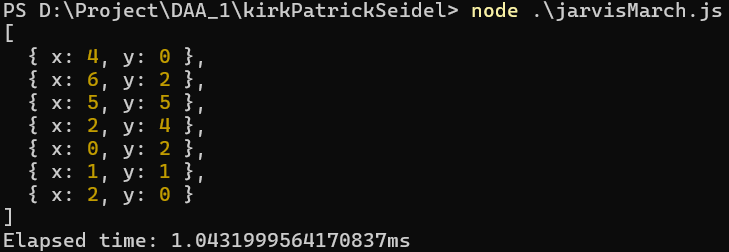
Input Points:
{ x: 0, y: 2 }, { x: 4, y: 4 }, { x: 4, y: 0 }, { x: 6, y: 2 }, { x: 2, y: 4 }, { x: 2, y: 0 }, { x: 3, y: 3 }, { x: 4, y: 0 }, { x: 5, y: 5 }, { x: 1, y: 1 }
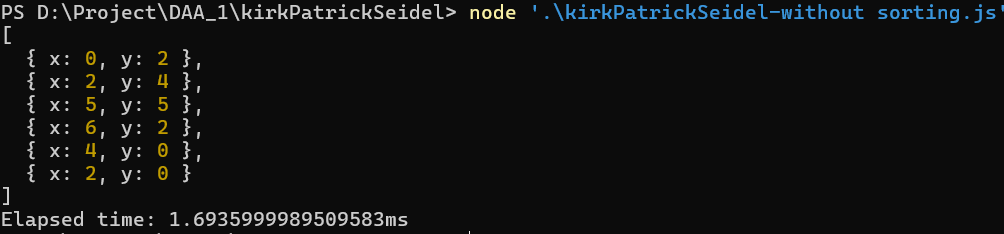
Input Points:
{ x: 2, y: 1 }, { x: 4, y: 3 }, { x: 6, y: 5 }, { x: 1, y: 3 }, { x: 3, y: 1 }, { x: 5, y: 4 }, { x: 0, y: 2 }, { x: 2, y: 4 }, { x: 4, y: 0 }, { x: 6, y: 2 }
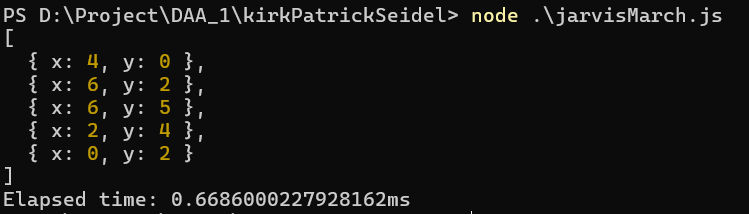
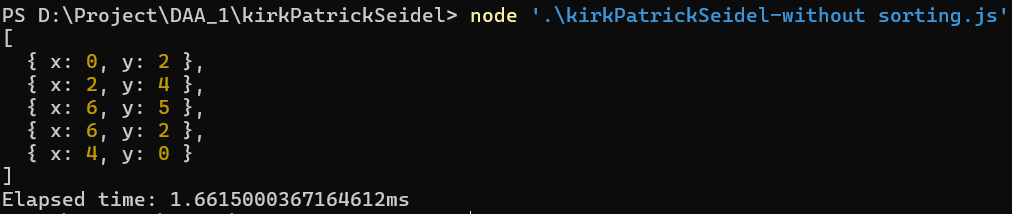
Input Points:
{ x: 1, y: 1 }, { x: 2, y: 3 }, { x: 4, y: 1 }, { x: 3, y: 5 }, { x: 5, y: 2 }, { x: 2, y: 4 }, { x: 6, y: 6 }, { x: 0, y: 2 }, { x: 3, y: 1 }, { x: 1, y: 4 }, { x: 4, y: 3 }, { x: 2, y: 1 }, { x: 5, y: 5 }, { x: 4, y: 0 }, { x: 0, y: 4 }
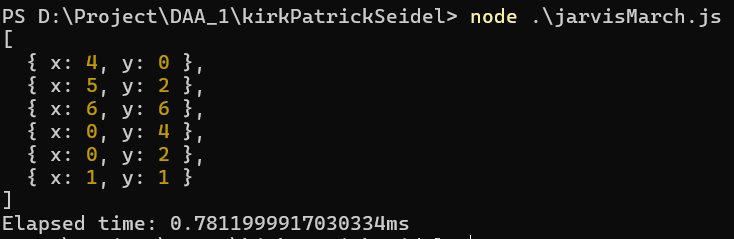
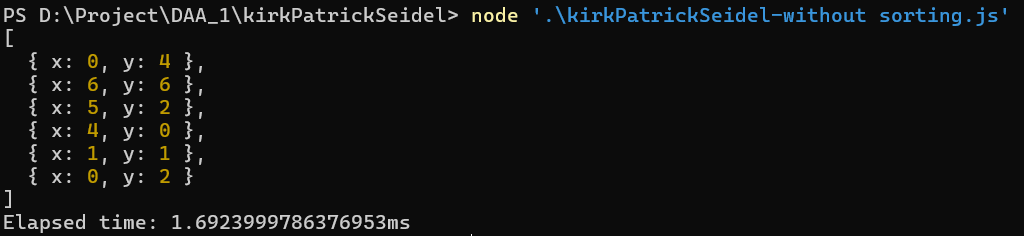
Input Points:
{ x: 2, y: 3 }, { x: 5, y: 1 }, { x: 3, y: 5 }, { x: 4, y: 2 }, { x: 1, y: 4 }, { x: 6, y: 6 }, { x: 0, y: 2 }, { x: 3, y: 1 }, { x: 4, y: 0 }, { x: 6, y: 4 }, { x: 2, y: 1 }, { x: 5, y: 5 }, { x: 0, y: 3 }, { x: 2, y: 4 }, { x: 4, y: 6 }
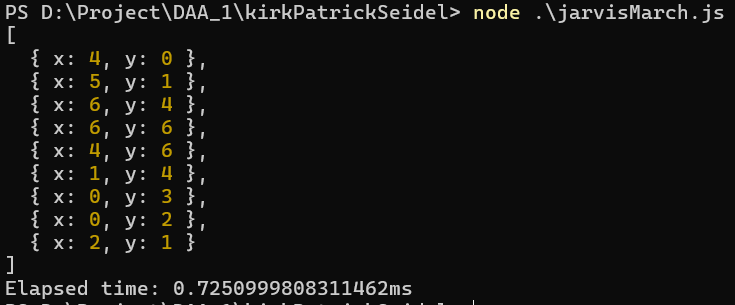
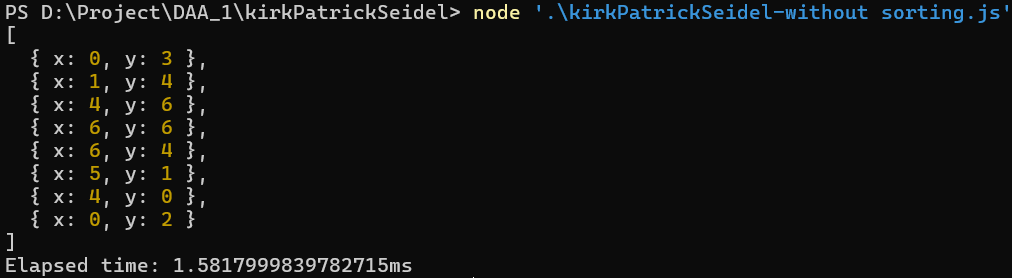
Observations:
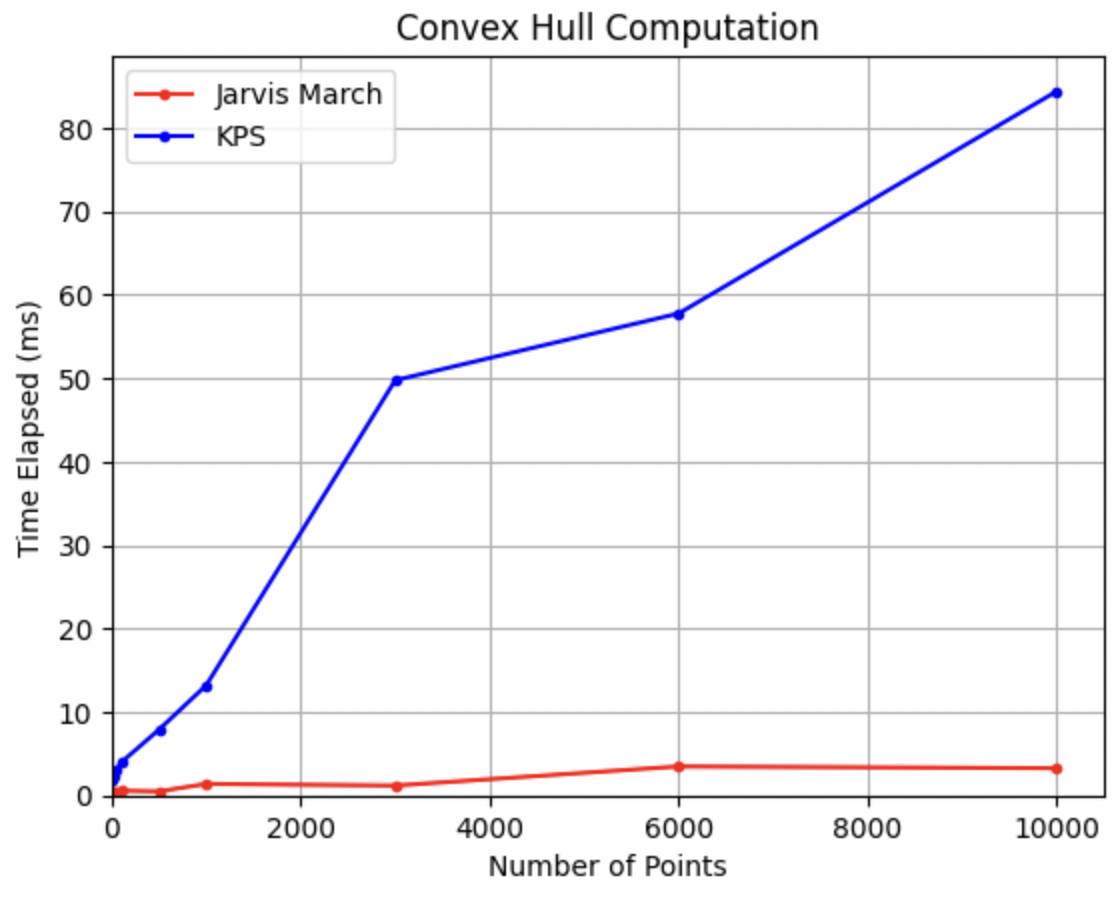
From the above results obtained by running given sets of points on both the Convex Hull Algorithms,
we can see that the Jarvis March algorithm outperforms the Kirkpatrick-Seidel algorithm significantly
in all cases. This could be attributed to the fact that the value of 'n', or number of points in the
point set we have considered is quite small. However, for large datasets, it is quite likely that the
opposite will be observed, and the efficiency of KPS for large 'n' will become apparent.
Time Complexity Analysis:
Kirkpatrick-Seidel
Kirk-patrick-seidel is a divide and conquer algorithm. The upperHull and lowerHull functions are
recursively called on the set of points until the size of the set reaches a base case
(less than or equal to 2). In each recursive call, the median splits the data points into 2 equal
sets of Tleft and Tright and hence for a set of size n to be divided into a set of size 2 or lesser
we need log(h) recursive calls, since the tree constructed can have a height of atmost 'h', where h
is the number of convexHull points.
Now, at each recursive call we have:
Finding the median x-coordinate: O(n) in the worst case.
Partitioning the set: O(n)
Bridge finding (upperBridge and lowerBridge): O(n) on average
Filtering points: O(n)
Therefore, the overall complexity is O(nlogh).
Jarvis March
The loop runs until the current point becomes the initial point again. Therefore, there are h iterations of the loop where h is the number of points in the convex-hull.and at each iteration there are n-1 comparisons (with every other point) to find the next point of the convex-hull. therefore , the time complexity is: O(h(n-1)) = O(hn)
Comparison of Time Elapsed in Computation of Convex Hull
Jarvis March
Number of input points |
Elapsed Time |
|---|---|
| 10 | 0.3626999855041504 ms |
| 20 | 0.3461000919342041 ms |
| 50 | 0.3661000728607178 ms |
| 100 | 0.5730001926422119 ms |
| 500 | 0.4872000217437744 ms |
| 1000 | 1.3842999935150146 ms |
| 3000 | 1.181800127029419 ms |
| 6000 | 3.474100112915039 ms |
| 10000 | 3.26170015335083 ms |
KPS
Number of input points |
Elapsed Time |
|---|---|
| 10 | 1.8460001945495605 ms |
| 20 | 2.3369998931884766 ms |
| 50 | 3.132999897003174 ms |
| 100 | 3.9646999835968018 ms |
| 500 | 7.891000032424927 ms |
| 1000 | 13.206400156021118 ms |
| 3000 | 49.752699851989746 ms |
| 6000 | 57.75859999656677 ms |
| 1000 | 84.37769985198975 ms |